El ejemplo clásico de una función recursiva es elcálculo del factorial de un número. Por ejemplo, 4! (factorial)es igual a 4 X 3 X 2 X 1. Algebraicamente, podemos considerar un factorial como(n!) as n X (n-1) X (n-2) X (n-3)...(n - (n+1)). Ésta sería ladefinición recursiva del factorial:

(defun factorial (n)
  (cond	((zerop n) 1)
	 (T 
    (* n (factorial (1- n))))
  ) ;_ fin de cond
) ;_ fin de defun

Se analizan dos condiciones:

1. que el argumento recibido sea cero (predicado ZEROP). En ese casose devuelve 1.
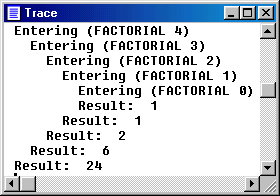
2. en cualquier otro caso, se multiplica el argumento por el resultado quedevuelve aplicar de nuevo la función de usuario factorial alargumento menos 1. Lógicamente la evaluación de estaoperación deberá esperar al resultado de la nueva llamada a lafunción factorial, que si aún no es cero,provocará una nueva llamada a la misma función factorial y quedará a la espera de que esta sea evaluada y asísucesivamente. Al llegar a cero el argumento pasado a factorial, ya nose producirá una nueva llamada a la función y se comenzaráa devolver respuestas a todas la evaluaciones que han quedado pendientes. Estecomportamiento puede verse claramente en la ventana TRACE de visuaLISP, después de haber evaluado la función (trace factorial) .

La recursión, aunque aporta soluciones de gran elegancia, debe serutilizada con cautela. Lo ideal sería usarla con funciones que noutilicen, o utilicen muy pocos argumentos, ya que la recursión colocacada vez una nueva copia de la función en la memoria de pila junto consus argumentos. Es muy posible que una función efectúe tantasrecursiones que se agote la memoria disponible provocando un error dedesbordamiento de la pila.

Para más detalles, consultar el artículoWHAT IS RECURSION? de Glenn Grotzinger.

ANÁLISIS DE UNA FUNCIÓN RECURSIVA

La siguiente función demuestra la posibilidad de desarrollarfunciones de usuario a partir de un corto número de primitivas. Lafunción BUSCA_EN_LISTA recibe como argumentos una expresióncualquiera y una lista. En caso que la expresión esté contenidaen la lista, la función devolverá la expresión y todos lostérminos de la lista que ocurren después de la expresión.Si expresión no pertenece a la lista, la función devuelve nil.Los resultados obtenidos son los mismos que los de la función primitivaMEMBER. De hecho muchas de las funciones hoy incorporadas a cualquiera de losdialectos modernos de LISP surgieron como funciones utilitarias que eranincorporadas de manera habitual por los usuarios.

;;;Función recursiva busca_en_lista.
;;;Equivale a la función member de LISP
;;;Esta función ha sido adaptada del tutorial
;;;LISP del ELM Research Group
(defun busca_en_lista (expresion lista)
  (cond
    ((null lista) nil)                         ;si lista está vacía o se acaba
    ((equal expresion (car lista)) lista)      ;si se encuentra expresion
    (t (busca_en_lista expresion (cdr lista))) ;en otro caso se efctúa la 
                                               ;recursión
  )
)

_$ (busca_en_lista '(a b) (list 2 r "sdf" '(a b) "KLM" 77 21 jfk))
((A B) "KLM" 77 21 nil)
_$ (member '(a b) (list 2 r "sdf" '(a b) "KLM" 77 21 jfk))
((A B) "KLM" 77 21 nil)
_$ 

Si antes de ejecutar esta función invocamos la función TRACE:

(trace busca_en_lista)

podemos seguir en la ventana TRACE de Visual LISP los pasos seguidos en laevaluación de esta función:

Entering (BUSCA_EN_LISTA (A B) (2 nil "sdf" (A B) "KLM" 77 21 nil))
  Entering (BUSCA_EN_LISTA (A B) (nil "sdf" (A B) "KLM" 77 21 nil))
    Entering (BUSCA_EN_LISTA (A B) ("sdf" (A B) "KLM" 77 21 nil))
      Entering (BUSCA_EN_LISTA (A B) ((A B) "KLM" 77 21 nil))
      Result:  ((A B) "KLM" 77 21 nil)
    Result:  ((A B) "KLM" 77 21 nil)
  Result:  ((A B) "KLM" 77 21 nil)
Result:  ((A B) "KLM" 77 21 nil)

Los objetivos perseguidos implican el recorrido de la lista, elemento aelemento, comparando cada uno con la expresión dada. La maneramás sencilla para extraer un elemento de la lista (el primero) esutilizar la función CAR. Un segundo elemento pudiera extraerse con CADRy así sucesivamente. Pero este método sería demasiadorígido si queremos que la función sea aplicable a una lista decualquier longitud.

Una solución estaría en que si el primer elemento no es elbuscado, volviéramos a ejecutar la función pero que esta vez elsegundo argumento (lista) fuera el resto de la lista, quitando el primertérmino ya analizado: (cdr lista).

Así continuaríamos probando el primer término (CAR dela lista) del resto (CDR) de la lista hasta que o termine la lista o que elprimer término sea el elemento buscado.

Las condiciones que se prueban corresponden a los tres casos posibles alsuministrar a la función BUSCA_EN_LISTA dos argumentos, el primero delos cuales puede ser un átomo o una lista y el segundo debe evaluar comouna lista, incluso vacía.

Primer caso: ((null lista) nil)

Cuando se encuentra esta condición, la evaluación termina. La función evaluará en este caso como nil, señalando que el término no ha sido encontrado. Este sería también el caso si el segundo argumento fuera una lista vacía.

Segundo caso: ((equal expresion (car lista)) lista)

Al igual que en el primer caso, la evaluación termina. Pero en este caso el primer término de la lista (car lista) es el término buscado, y se devuelve el valor de lista.

Tercer caso: (t (busca_en_lista expresion (cdr lista)))

Este es el caso en que se produce la recursión. Siempre que lista noesté vacía (null lista) y que el primer elemento de lista no seaigual al término buscado, se llama de nuevo a la funciónBUSCA_EN_LISTA pero esta vez se le pasa como argumento lista (cdr lista), elresto de la lista, desechando el primer término. Así a cadaciclo, lista se acorta en un término. Al final, si expresion no formaraparte de lista, la recursión terminaría al llegar a ser una listanula.

Si observamos lo devuelto en la ventana TRACE por una y otra de estas dosfunciones recursivas, observamos una diferencia. Lo devuelto por elúltimo nivel de recursión en la función FACTORIAL esdiferente a lo devuelto por el nivel superior. De hecho cada nivel devuelve unresultado diferente. Para llegar al resultado definitivo, debemos esperar a loque devuelve cada uno de los ciclos de la recursión. Sin embargo, en lasegunda función BUSCA_EN_LISTA, el resultado del último nivel esya el resultado definitivo. Es evidente que resulta una pérdida detiempo el esperar a que cada nivel devuelva ese mismo resultado hasta llegar alnivel superior. Los compiladores LISP más avanzados reconoceránuna función de este tipo y cortarán el proceso en el instante quese obtiene el resultado del último nivel, mejorando sustancialmente lavelocidad de operación de las funciones. Este tipo de funcionesrecursivas se conocen por el término inglés de TAIL-RECURSIVE (~recursivas por la cola).

En muchos casos, hacer una función recursiva por la cola(tail-recursive) es posible empleando técnicas adecuadas deprogramación. Siempre que esto se logre podemos esperar un incrementosignificativo en la eficacia de los programas.

Nota: Según afirma Reini Urban, VLISP no es capaz de reconocer larecursividad por la cola o tail-recursion, de manera que aún resulta enuna utilización exhaustiva de la memoria de pila (stack). Sobre loslímites valores máximos admitidos de anidación(tamaño de pila) dicho autor propone ejemplos enhttp://xarch.tu-graz.ac.at/autocad/stdlib/STDINIT2.LSP

SU UTILIZACIÓN PRÁCTICA DENTRO DE AUTOCAD

Como ejemplo de la utilidad de los métodos de programaciónexpuestos, desarrollaremos un programa encaminado a resolver un problemaconcreto dentro de la aplicación. En ocasiones tenemos la necesidad deextraer la información de las coordenadas de los vértices de unapolilínea. En este caso analizaremos una polilínea del tipoLWPOLYLINE, que se introdujo con la versión 14 de AutoCAD. Las entidadesde AutoCAD guardan su información en forma de listas deasociación, una lista con sublistas donde el número inicial decada sublista identifica el tipo de dato de que se trata. Un proceso recursivosería especialmente adecuado para recorrer dicha lista extrayendo deella la información requerida. Pasaremos entonces a estudiar eldesarrollo de una FUNCIÓN RECURSIVA PARA LALECTURA DE LOS VÉRTICES DE UNA POLILÍNEA