por Reinaldo Togores Fernández <reinaldo.togores@unican.es>
Este artículo fué publicado en el número 53,febrero-marzo 1998 de AUTOCADMagazine.
- Sistemas de Coordenadas
- Vector normal y definición del SCO
- Transformación de coordenadas entresistemas
- Descripción del Programa
En nuestro artículo anterior (AUTOCAD Magazine, número 49),proponíamos un programa para la conversión de polilíneas3D en polilíneas 2D. Dicho programa poseía una limitación:sólo operaba sobre polilíneas 3D contenidas en el plano XY o enplanos paralelos a él. El motivo de esta limitación reside en ladiferente manera en que se expresan las coordenadas de los vértices delas polilíneas 3D y 2D. En las primeras, los vértices se expresanen coordenadas referidas al Sistema de Coordenadas Universal (SCU). En lassegundas las coordenadas estarían expresadas en el Sistema deCoordenadas de Objeto (SCO) de cada entidad particular. Ambos sistemassólo coincidirían en caso de que el SCO sea idéntico alSCU. Aún cuando este análisis tenía en cuenta sólolas polilíneas clásicas, lo mismo vale para las polilíneasoptimizadas de la versión 14. Como prometimos entonces, en este segundoartículo abordamos la problemática de aplicar dichaconversión a polilíneas 3D coplanares situadas en cualquierposición en el espacio.
 I. Sistemas de Coordenadas:
I. Sistemas de Coordenadas:
Comenzaremos por una breve discusión de los sistemas de coordenadasimplicados.
Examinemos los datos utilizados por AutoCAD para definir dos entidades 2D,en este caso círculos, con el centro en el mismo punto del espacio,contenido uno de ellos (que llamaremos A) en el plano XY del SCU y el otro (B)en un plano paralelo al plano XY de un Sistema de Coordenadas Personales (SCP)definido a partir de un giro de 45º en torno al eje Y"Universal".
| Lista de entidad Círculo A: | Lista de entidad Círculo B: | |
( | ( | |
| Nombre de Entidad | (-1 . <Entity name: 25e0558>) | (-1 . <Entity name: 25e0560>) |
| Tipo de Entidad | (0 . "CIRCLE") | (0 . "CIRCLE") |
| Identificador | (5 . "2B") | (5 . "2C") |
| Subclase | (100 . "AcDbEntity") | (100 . "AcDbEntity") |
| Espacio | (67 . 0) | (67 . 0) |
| Capa | (8 . "0") | (8 . "0") |
| Subclase | (100 . "AcDbCircle") | (100 . "AcDbCircle") |
| Centro | (10 10.0 10.0 0.0) | (10 10.0 -7.07107 7.07107) |
| Radio | (40 . 5.0) | (40 . 5.0) |
| Vector Normal | (210 0.0 0.0 1.0) | (210 0.707107 0.0 0.707107) |
De la lista de asociación identificada con el código 10obtenemos con (cdr (assoc 10 lista_entidad)) la información quecorresponde a las coordenadas del centro del círculo.
- Círculo A: X=10.0 Y=10.0 Z=0.0
- Círculo B: X=10.0 Y=-7.07107 Z=7.07107
Pero este centro que genera dos series de valores XYZ diferentes es enrealidad el mismo punto. Más aún, si investigamos el valor de suscoordenadas utilizando el comando ID obtendríamos:
- En el SCU: X=10.0000 Y=10.0000 Z=0.0000
- En el SCP: X=7.0711 Y=10.0000 Z=7.0711
El resultado es harto sorprendente: Tres valores distintos (a-c, b y d) paraun mismo punto del espacio. La explicación reside en que los tresvalores resultan de los tres sistemas diferentes en que dichas coordenadas seexpresan:
- Sistema de Coordenadas Universales (SCU):
es el sistema "de referencia", en función del cual se definentodos los demás. Este sistema es siempre el mismo, por lo que losvalores medidos con respecto a él permanecen constantes cuando se pasa aotros sistemas. Es el valor que obtenemos en respuesta al comando ID estandoactivo el SCU.
- Sistema de coordenadas Personales (SCP):
es el sistema "de trabajo". El usuario puede especificar en cadamomento el SCP mas adecuado a las tareas de dibujo que realiza. Todos lospuntos que se transmiten a los comandos de AutoCAD, incluidos los devueltos porfunciones externas y rutinas de AutoLISP, están en el sistema SCP actual(a menos que el usuario los preceda de un * en la solicitud Comando). Losvalores que obtuvimos a partir del comando ID son fácilmente explicablesteniendo en cuenta el giro de 45º en torno al eje Y de nuestro SCP(resultando el valor de X e Y=10 x cos 45).
- Sistema de Coordenadas de Objeto (SCO):
en este sistema, que hace referencia al propio objeto, se expresan los valoresde los puntos en la lista de entidad (grupos DXF 10 al 37) devuelta por lafunción ENTGET.
 II. Vector normal y definicióndel SCO:
II. Vector normal y definicióndel SCO:
Observemos el otro campo en que difieren los registros de entidad de amboscírculos:
| Vector Normal: | (210 0.0 0.0 1.0) | (210 0.707107 0.0 0.707107) |
El código 210 identifica el vector unitario normal, un vector3D de longitud igual a la unidad que describe (salvo excepciones que másadelante señalaremos) el eje Z del SCO.
Para una dirección dada del eje Z o extrusión, hay unnúmero infinito de sistemas de coordenadas, definidas mediante latraslación del origen en el espacio 3D y la rotación delos ejes X e Y en torno al eje Z. Sin embargo, para una direccióndel eje Z, hay un único SCO que se define a partir de lossiguientes criterios:
- Su origen coincide con el origen del SCU.
- La orientación de los ejes X e Y dentro del plano XY se calculan deuna manera que es descrita en la documentación de AutoCAD como"arbitraria pero consistente", mediante el llamado Algoritmo de EjeArbitrario, cuya discusión haría demasiado extensa estaexposición.
Estos dos criterios explican que el SCO no coincida necesariamentecon el SCP vigente en el momento de dibujarse la entidad. Y de ahí losvalores discordantes que pueden obtenerse para los puntos de una entidadsegún se investiguen con comandos como ID y LIST o provengan de lalectura de la lista de entidad del objeto que se obtiene a partir de lafunción ENTGET, aún cuando la lectura de esos valores se realiceestando vigente el mismo SCP en que fue dibujada originalmente la entidad.Obviamente, será necesario convertir siempre a coordenadas del SCO losvalores de los puntos que se pasen a las funciones ENTMOD o ENTMAKE para lamodificación de estas entidades o para la creación de otrasnuevas de las mismas características.
En algunos casos el SCO coincidirá con el SCU. Este es el caso de lasentidades 3D, es decir, las entidades que pueden dibujarse en planos noparalelos al plano XY del SCP actual. Estas entidades incluyen líneas,puntos, 3Dcaras, polilíneas y vértices 3D, mallas yvértices de mallas 3D y splines. En todos estos casos, los valores XYZestarán dados con referencia al SCU.
No sucede lo mismo con las Entidades 2D (círculo, arco, sólido2D, trazo, texto, atributo y definición de atributo, forma,inserción de bloque, polilínea 2D, vértice 2D) quesólo pueden dibujarse en el plano XY del SCP actual o en planosparalelos al mismo. Sus coordenadas se expresan siempre en valores referidos alSCO.
Al referirnos más arriba al significado del código 210 lodescribíamos como vector normal que permite definir la direcciónZ del SCO. El vector normal que describiría el SCU estaría dadopor la lista de tres números reales (0.0,0.0,1.0). Pero el dato de lalista asociada al código 210 no nos permite siempre determinar si el SCOy el SCU coinciden. Será necesario tener en cuenta una serie deexcepciones en que el valor asociado a este código sería mejordescrito como vector de extrusión. En general, las entidades 3D nopueden tener "Altura de Objeto". Se dan dos excepciones a esta regla:la línea y el punto. En ambas entidades este vector no representa elsistema de coordenadas que definen su posición en el espacio, sino ladirección del vector normal del SCP en que dichas entidades fueroncreadas y que sirve para determinar la dirección en el espacio en que seproducirá su "extrusión" al establecerse un valordiferente de cero para su Altura de Objeto. Aunque no es susceptible de serextruída, también presenta una "anomalía" deeste tipo la entidad SPLINE cuando la misma es coplanar. Cuando en la lista deentidad no aparece este código, se sobreentiende que sus coordenadasestán referidas al SCU.
 III. Transformación decoordenadas entre sistemas
III. Transformación decoordenadas entre sistemas
Para la conversión entre sistemas de coordenadas AutoLISP dispone dela función TRANS:
(trans pto orig dest [desp])
En el caso que nos ocupa, la conversión se haría desde elSCU (ya que nos proponemos transformar una entidad 3D) al SCO quecorrespondería al plano que contiene los vértices de la3DPOL. La función TRANS admite como primer argumentopto un punto o vector de desplazamiento (lista de tres númerosreales), un segundo argumento orig que indica el sistema de coordenadasal que se refieren los valores de pto, y un tercer argumento destque especifica el sistema de coordenadas al que se transformarán losvalores de pto. Un cuarto argumento opcional desp indica, si esdistinto de cero que se trata de un vector en lugar de un punto.
En el caso que nos ocupa. La función trans se aplicaría a lascoordenadas de cada vértice (dato asociado al código 10 de lalista de entidad) y el sistema de coordenadas de origen siempre sería,según hemos explicado más arriba, el SCU. El problemaestaría en definir cuál sería el SCO quecorrespondería a la nueva entidad Polilínea 2D que pretendemosconstruir. Analicemos para ello las formas de especificar los sistemas decoordenadas que acepta la función TRANS.
| Sistema de Coordenadas: | Especificación: |
| Universal SCU | 0 |
| Personal SCP | 1 (SCP actual) |
| Pantalla SCV | 2 (actual) |
| E. Papel SCVEP | 3 (sólo en combinación con elcódigo 2) |
| Objeto SCO | Un nombre de entidad (asociado al código–1 en la lista de entidad) Un vector de extrusión (vectorunitario normal 3D) |
Como no tenemos aún una entidad a la que podamos recurrir paraidentificar el SCO empleando el primer procedimiento, no habrá otravía que la de acometer el cálculo del vector normal al plano quecontiene la polilínea original. Como se trata de una polilínea3D, lo primero que tendremos que hacer será asegurarnos que todos susvértices se encuentran en el mismo plano. De no ser así, laconversión sería imposible.
El procedimiento a seguir sería:
- Extraer de la entidad seleccionada la lista de sus vértices.
- Extraer de dicha lista de vértices tres que no sean colineales.
- Comprobar que cada uno de los vértices restantes se encuentresituado en el plano definido por los tres vértices seleccionados en elpaso anterior, es decir que sean coplanares.
- Si la condición anterior se cumple, calcular el vector normal alplano y proceder a la conversión.
Dichos procedimientos se abordarán como funciones de libreríade uso general, susceptibles de ser incorporadas a cualquier programa.
 IV. DESCRIPCIÓN DEL PROGRAMA
IV. DESCRIPCIÓN DEL PROGRAMA
Función extpt
Función colineal
Función trio
Función plano
Función normal
Función test
 Función extpt:Extracción de la lista de vértices.
Función extpt:Extracción de la lista de vértices.
Prepara una lista de puntos a partir de las listas de entidad"POLYLINE". Debe ser llamada desde una función que compruebeque se trata de una polilínea (2D o 3D) y obtenga lista de entidad quedebe pasar a esta función como argumento. Establece un bucle que terminaal encontrar la entidad SEQEND. Devuelve la lista de valores asociados alcódigo 10 de cada vértice. Utiliza la variable local tmplst .
(defun extpt ( lista_ / tmplst ) (while (/= (cdr (assoc 0 (setq lista_ (entget (entnext (cdr (assoc -1 lista_)))) ) ) ) "SEQEND" ) (setq tmplst (cons (cdr (assoc 10 lista_)) tmplst)) ) (setq tmplst (reverse tmplst))) Función colineal:Comprobación de la Colinealidad.
Función colineal:Comprobación de la Colinealidad.
El algoritmo empleado para determinar la condición de colinealidadparte de la consideración de las propiedades de los vectoresdeterminados por tres puntos no coincidentes.
En un sistema tridimensional de coordenadas rectangulares podemosrepresentar los vectores unitarios desde el origen a los puntos (1,0,0),(0,1,0) y (0,0,1) por i, j yk. Cualquier vector en el espacio puede ser representadoen función de estos vectores unitarios. De esta manera, el vector desdeel origen al punto A(a,b,c) será:
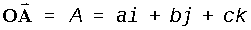
Los vectores ai, bj, y ckson los componentes x, y, z, del vector A. La longitud del vector A puedeobtenerse a partir de las longitudes de los lados de los triángulosrectángulos OCA y ODC (Fig. 1).
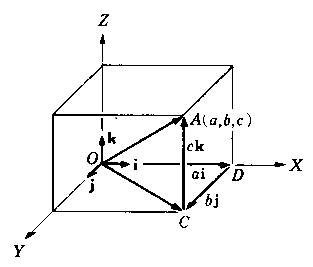
(OA)2=(OC)2 +(CA)2
=(OD)2 + (DC)2 +(CA)2
=a2 + b2 + c2.
De aquí que la longitud de A sea:
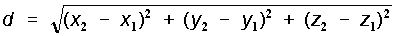
Generalizando el caso, un vector entre cualesquiera dos puntos del espacio, P1(x1,y1,z1) yP2(x2,y2,z2)tendría los componentes (x2-x1)i , (y2-y1)j, ( z2-z1)k y serepresentaría mediante la expresión (Fig. 2):
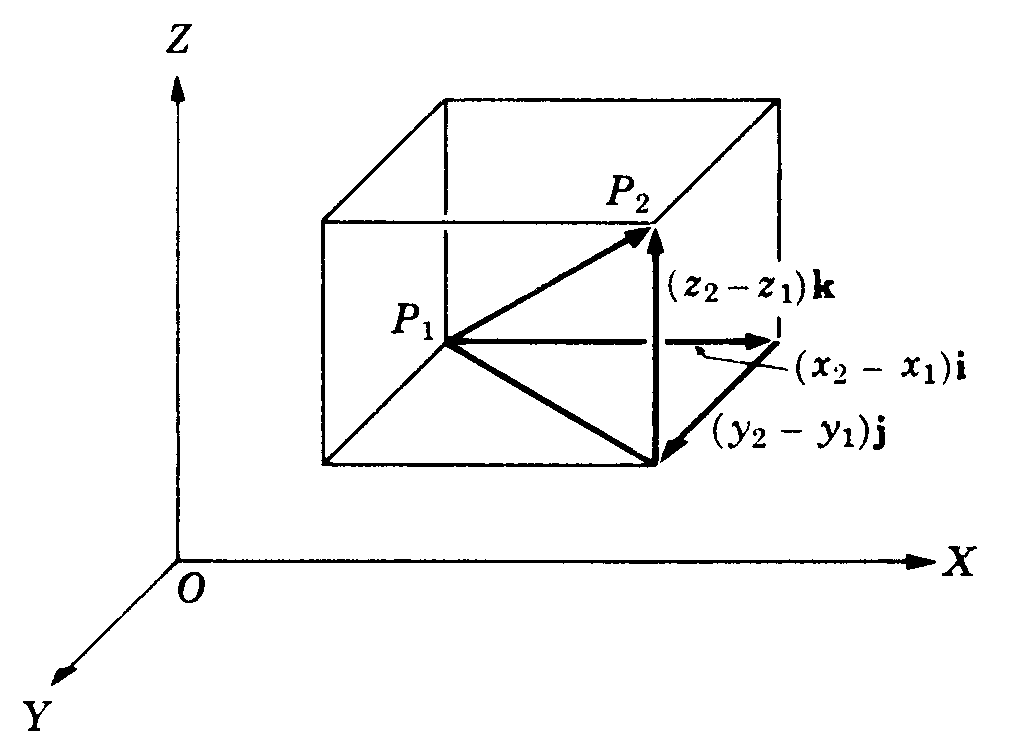
P1P2=(x2-x1)i+(y2-y1)j+ (z2-z1)k
Y su longitud, la distancia entre P1 y P2,sería:
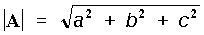
El criterio que nos permitirá detectar la colinealidad de los trespuntos examinados se deriva de la formulación del productoescalar de dos vectores:
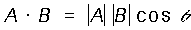
Donde q es el ánguloentre los vectores si se trazaran desde un origen común. Los puntosserían colineales cuando cosq =1 en:
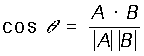
El producto A·B se obtendrá mediante:
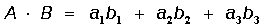
De ahí que si se cumple que:
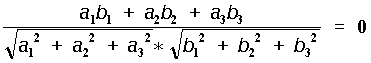
podemos afirmar que los vectores A y B son colineales.
El programa toma los tres primeros puntos de la lista que recibe comoargumento y determina los valores de los coeficientes a1,a2 y a3 del primer vector y los coeficientes b1, b2 y b3 del segundo, sustituyendodichos valores en la ecuación anterior. Si la condición es ciertadevuelve T y si es falsa nil.
(defun colineal ( ptlist / )(setqp1 (car ptlist)p2 (cadr ptlist)p3 (caddr ptlist);;Vector A = p1->p2a1 (- (car p2)(car p1))a2 (- (cadr p2)(cadr p1))a3 (- (caddr p2)(caddr p1));;Vector B = p1->p3b1 (- (car p3)(car p1))b2 (- (cadr p3)(cadr p1))b3 (- (caddr p3)(caddr p1)))(if(equal(abs(/(float(+ (* a1 b1)(* a2 b2)(* a3 b3)))(*(sqrt (float (+ (expt a1 2) (expt a2 2) (expt a3 2))))(sqrt (float (+ (expt b1 2)(expt b2 2)(expt b3 2)))))))10.00000001)Tnil))
Sólo cabría observar que la igualdad se comprueba mediante lafunción EQUAL, que permite establecer un pequeñomargen de error teniendo en cuenta el redondeo de las cifras en las operacionesefectuadas con números reales.
![]() Función trio:selección de tres vértices no colineales.
Función trio:selección de tres vértices no colineales.
Esta función recorre la lista de vértices de tres en treshasta encontrar aquéllos que pasados a la función colineal antes descrita obtengan nil como resultado. En el caso de que lalista incluya solamente dos vértices, o que todos los vérticesfueran colineales (lo que implica que serán también coplanares),se construirá un vértice de manera arbitraria con el objetivo depoder definir uno de los infinitos planos que contienen a dichosvértices. Cualquier punto del espacio sería válido. Eneste caso hemos optado por incrementar en la unidad el valor de X delúltimo vértice.
;;Función trio (defun trio (ptlist / tmplst) (setq tmplst ptlist) (cond ((= (length tmplst) 2) ;;Si sólo hay dos vértices, (setq p1 (car tmplst) p2 (cadr tmplst) p3 ;;se construye uno arbitrario. (list (1+ (car (last tmplst))) (cadr (last tmplst)) (caddr (last tmplst)) ) ) ) ((= (length tmplst) 3) (setq p1 (car tmplst) p2 (cadr tmplst) p3 (last tmplst) ) ) ;;mientras sean más de tres ;;y sean colineales… (t (while (and (colineal tmplst) (> (length tmplst) 3)) (setq tmplst (cdr tmplst)) ) ) ) ;;Si todos son colineales, ;;se modifica el tercer vértice (if (colineal (list p1 p2 p3)) (setq p3 (list (1+ (car p3)) (cadr p3) (caddr p3))) )) Función plano:Comprobación de la Coplanaridad:
Función plano:Comprobación de la Coplanaridad:
De los puntos incluidos en la lista la función trio haseleccionado los tres primeros vértices no colineales. A partirde ellos se determinará la fórmula del lugar geométricodel plano. Para hacerlo tendremos en cuenta que un vector perpendicular a doslados del triángulo definido por dichos tres vértices seráel vector normal al plano que contiene el triángulo en cuestión.Para encontrar este vector planteamos que:
P1P2=(x2-x1)i+(y2-y1)j+(z2-z1)k
P1P3=(x3-x1)i+(y3-y1)j+(z3-z1)k
N=Ai + Bj + Ck
El problema consistiría en hallar los coeficientes A, B y C de maneraque N fuera perpendicular a los otros vectores. Así que:
N ·P1P2=(x2-x1)A+(y2-y1)B+(z2-z1)C=0
N ·P1P3=(x3-x1)A+(y3-y1)B+(z3-z1)C=0
Para simplificar el sistema, asignamos el valor de C=1. Una vezdeterminados los coeficientes A, B y C, se puede establecer la ecuacióndel plano:
Ax + By + Cz + D=0
Cualquier punto cuyas coordenadas XYZ satisfagan dicha ecuaciónpertenecerá al plano considerado.
(defun plano ( ptlist / tmplst resultado)(trio ptlist)(setq;;Hallar los coeficientes de la ecuación del plano:;;Ecuación vector 1->2: (x2-x1)A+(y2-y1)B+(z2-z1)C=0;;Ecuación vector 1->3: (x3-x1)A+(y3-y1)B+(z3-z1)C=0;;Despejando A en 1->2:;; A = (( -(y2-y1)B -(z2-z1)) / (x2-x1));;Despejando A en 1->3:;;A = ((-(y3-y1)B-(z3-z1)) / (x3-x1))
A;;Coeficiente A=(/(float(-(* (- (caddr p3)(caddr p1))(- (cadr p2)(cadr p1)))(* (- (caddr p2)(caddr p1))(- (cadr p3)(cadr p1)))))(float(-(* (- (car p2)(car p1))(- (cadr p3)(cadr p1)))(* (- (car p3)(car p1))(- (cadr p2)(cadr p1))))))
B ;;Coeficiente B =(/(float(-(* (- (caddr p3)(caddr p1))(- (car p2)(car p1)))(* (- (caddr p2)(caddr p1))(- (car p3)(car p1)))))(float(-(* (- (car p3)(car p1))(- (cadr p2)(cadr p1)))(* (- (cadr p3)(cadr p1))(- (car p2)(car p1))))))
D;;Coeficiente D:(-(+(* A (car p1))(* B (cadr p1))(caddr p1))))
;;Ahora se comprueban todos los puntos de la lista original contra;;la fórmula del plano(setq resultado T tmplst ptlist)(repeat (length tmplst)(if(equal(+(* A (car (car tmplst)))(* B (cadr (car tmplst)))(caddr (car tmplst))D)00.00000001)( )(setq resultado nil))(setq tmplst (cdr tmplst)))
resultado ;;La función devuelve cierto "T" o falso "nil")
 Función normal:Determinación del vector unitario normal.
Función normal:Determinación del vector unitario normal.
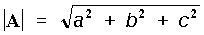
Una ecuación del tipo Ax + By + Cz + D=0 representa un plano perpendicular al vector N=Ai + Bj + Ck. De ahí que una vezconocidos los coeficientes A y B necesarios para determinar la ecuacióndel plano. Para obtener el vector unitario habrá que dividir dichoscoeficientes por la longitud del vector que respondería a larelación que vimos más arriba, obtenida a partir del teorema dePitágoras:
(defun normal ( A B / ) ;;Determinar el vector normal unitario (list (/ A (sqrt (+ (expt A 2) (expt B 2) (expt 1 2))) ) (/ B (sqrt (+ (expt A 2) (expt B 2) (expt 1 2))) ) (/ 1 (sqrt (+ (expt A 2) (expt B 2) (expt 1 2))) ) )) Función test: prueba de lasfunciones propuestas.
Función test: prueba de lasfunciones propuestas.
Para no hacer más extenso este artículo, considerando ya haberabusado más de la cuenta de la benevolencia de nuestros lectores,acabaremos integrando las funciones elaboradas a una pequeñafunción de prueba. Esta función informaría sobre lacoplanaridad de cualquier polilínea seleccionada, y de ser coplanar,suministraría los valores del vector unitario normal. Si se trata de unapolilínea 2D, pueden comprobarse estos valores con los asociados alcódigo 210 de la lista de entidad. En un próximo artículoaplicaremos estas funciones a la transformación de polilíneas 3Den polilíneas 2D cuando las primeras no resultaran paralelas al plano XYdel SCU.
(defun c:test () (if (plano (extpt (entget (car (entsel))))) (progn (alert "Los vértices de esta polilínea \nson coplanares") (setq vector_unitario (normal A B)) (alert (strcat "El vector normal unitario es: \n (" (rtos (car vector_unitario)) " " (rtos (cadr vector_unitario)) " " (rtos (caddr vector_unitario)) ")" ) ) ) (alert "Los vértices de esta polilínea \nNO son coplanares") ))


